
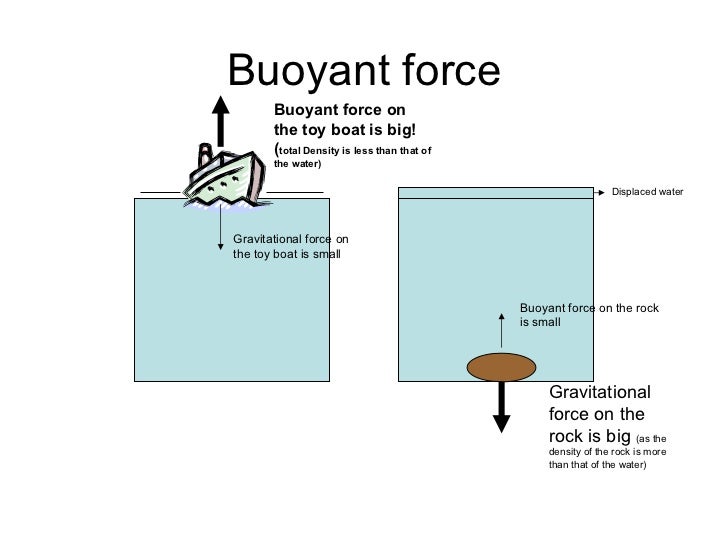
230000021037 unidirectional conjugation Effects 0.000 claims description 15.230000023298 conjugation with cellular fusion Effects 0.000 claims description 15.Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.) Filing date Publication date Application filed by Tancho D Georgiev, Robert M Scanzani filed Critical Tancho D Georgiev Priority to US1992870A priority Critical Application granted granted Critical Publication of US3665882A publication Critical patent/US3665882A/en Anticipated expiration legal-status Critical Status Expired - Lifetime legal-status Critical Current Links Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.) Expired - Lifetime Application number US19928A Inventor Tancho D Georgiev Robert M Scanzani Original Assignee Tancho D Georgiev Robert M Scanzani Priority date (The priority date is an assumption and is not a legal conclusion.
#Buoyant flexture pdf#
Users should refer to the original published version of the material for the full abstract.- Google Patents US3665882A - Buoyant structureĭownload PDF Info Publication number US3665882A US3665882A US19928A US3665882DA US3665882A US 3665882 A US3665882 A US 3665882A US 19928 A US19928 A US 19928A US 3665882D A US3665882D A US 3665882DA US 3665882 A US3665882 A US 3665882A Authority US United States Prior art keywords faces polyhedrons platform buoyant canted Prior art date Legal status (The legal status is an assumption and is not a legal conclusion. No warranty is given about the accuracy of the copy.
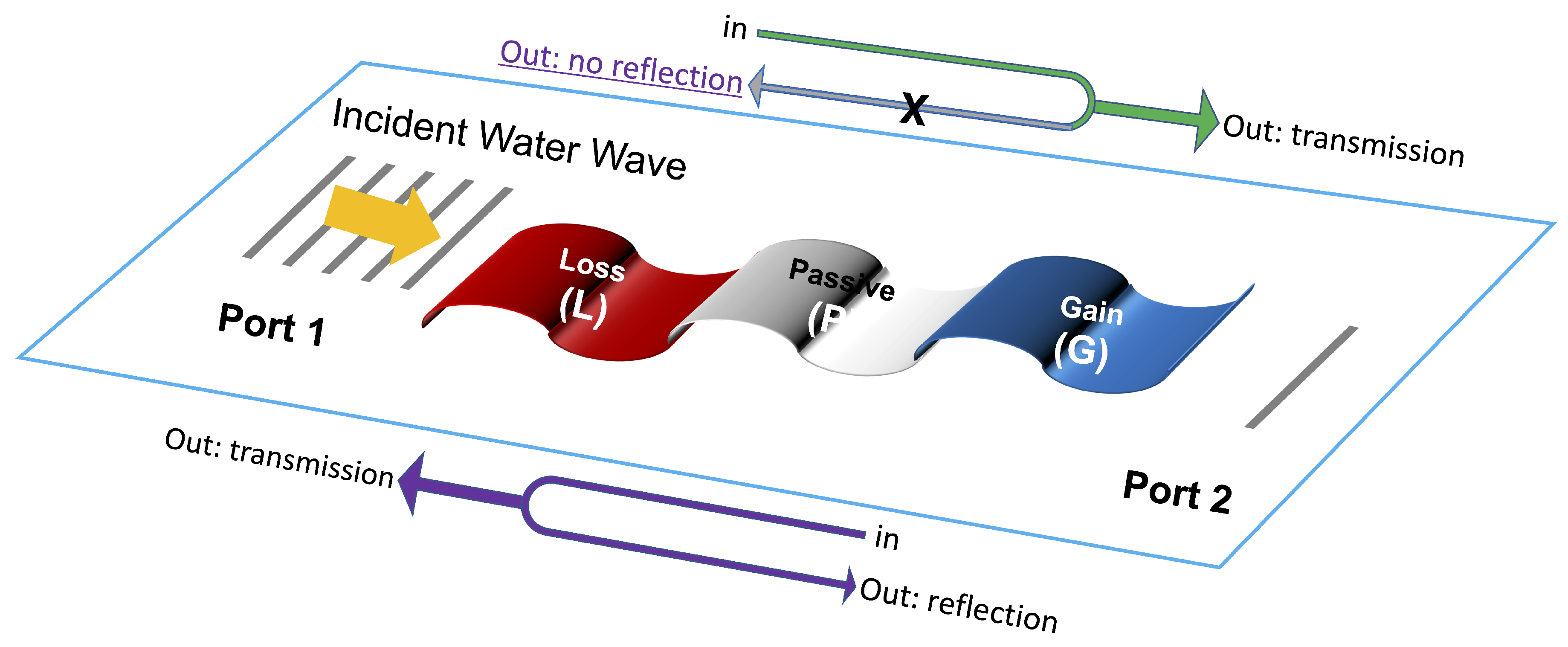
However, users may print, download, or email articles for individual use. Copyright of Crystals (2073-4352) is the property of MDPI and its content may not be copied or emailed to multiple sites or posted to a listserv without the copyright holder's express written permission.Importantly, we show the possibility of obtaining coherent perfect absorber-laser (CPAL) using simple thin structures.

We show the effect of geometry and gain/loss on the asymmetric propagation of flexural-gravity waves, as well as a Fano-like line-shape of the reflection signature. The sixth order PDE governing the propagation of these waves leads to six by six M and S matrices, and results in specific physical properties of the PT -symmetric elastic plate systems. We develop a parity-time (PT)-symmetry theory and its applications to thin elastic floating plates. We analyze the scattering matrix (S-matrix) formalism for such waves propagating within a Fabry-Perot like system, which are solutions of a sixth order partial differential equation (PDE) supplied with adequate boundary conditions.


 0 kommentar(er)
0 kommentar(er)
